

They should really include tests which take these factors into account. Walt Andersons gauges had a difference in their readings of about. The lowest psi registered at halftime was 10.5. That 80 degree air would cause the footballs to lose 1.6psi once they reached a temperature equilibrium with 48 degree air. What if they find out that normal prep and inflation in the equipment room causes the temperature in there to be more like 80 degrees? What if they find out that when the balls are then put into the ball bag (as they await transfer to the officials locker room for measurement) they retain that psi resulting from 80 degree air because the footballs are surrounded by other warm footballs inside a weatherproof ball bag? What if they find out that when the officials take the footballs out to measure, they do not allow enough time for the footballs to reach a temperature equilibrium with the 70 degree officials lockerroom.so that the psi being measured is actually a result of 80 degree air? Calculations have been updated.Yes, but keep in mind that the 1 psi drop was for a starting temperature of 70 degrees and a temperature equilibrium reached of 48 degrees.

enough to be considered massively underinflated.Įdit: As the poster noted below, forgot to account for the difference between gauge and absolute pressure. Granted, it's unlikely that anyone would inflate balls from 0, but it easily could cost another couple hundredths of a psi in pressure.įor a ball that barely meets specifications (12.5 psi gauge), it's pressure would drop to 11.1 psi during the game. Up to 0.25 additional psi can be lost if the balls were inflated by either the team or the refs prior to the game. At 49 degrees, the vapor pressure of water is 0.13 psi. If youve driven your car or it has been sitting in the sun, the resulting heat could raise your tires pressure by several PSI. The total pressure of the ball is equal to the pressure of the air inside the ball and the vaporized water in the ball. At 70 degrees, water has a vapor pressure of 0.38 psi. *Furthermore, given that it was raining all day, the air in the stadium was saturated with water vapor. At the game time temperature, the balls would have an absolute pressure of 26.2 psi and a gauge pressure of 11.5, below league specifications. We plug everything into the equation and get (27.7/294.1) = (P2/278). We are attempting to solve for the new pressure at this temperature, P2. The game time temperature was 49 degrees F (278 K). Since these are initial values, we will call them P1 and T1. This makes the absolute pressure of the ball 27.7 psi (gauge + atmosphere). Do a quick review on the ground once you add all those cold weather items to check your normal ra. Just a friendly reminder that the addition of long underwear, gloves,etc can change the way things feel from suit fit to ones hackey and handles. Let's assume an average ball has a gauge pressure of 13 psi. is apon us or soon to be depending on where you live. BTU is often used as a point of reference for comparing.
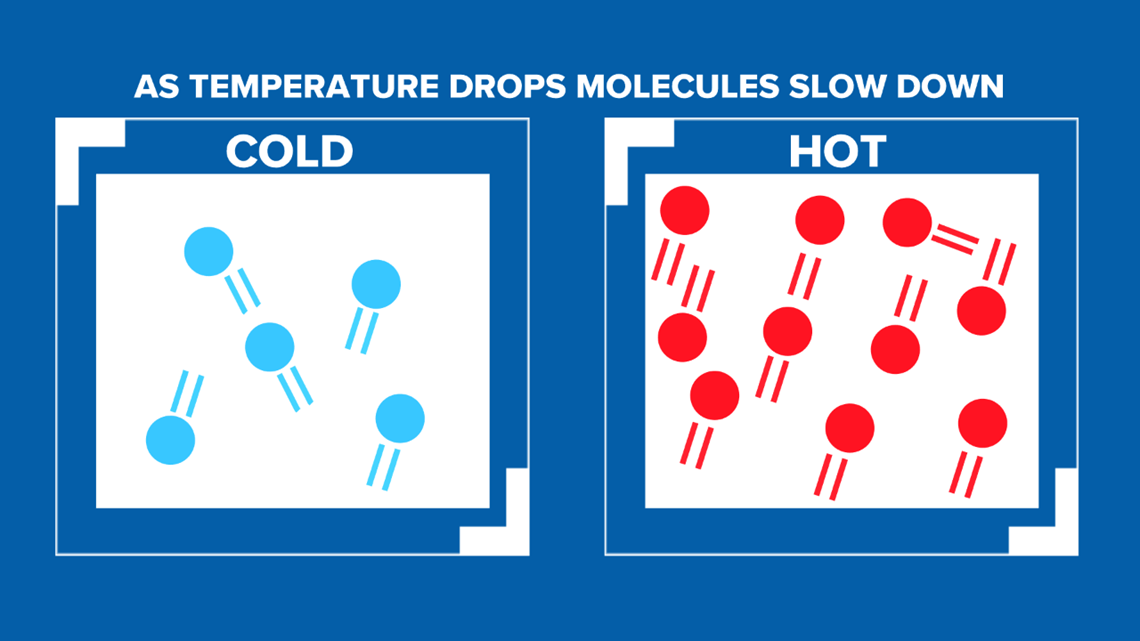
1 watt is approximately 3.412 BTU per hour. 1 BTU 1,055 joules, 252 calories, 0.293 watt-hours, or the energy released by burning one match. The calculator above uses the beer styles mean C02 value to calculate the recommended PSI setting. It is approximately the energy needed to heat one pound of water by 1 degree Fahrenheit. The balls are inflated to between 12.5 and 13.5 psi at a temperature of 70 degrees Farenheit (294.1 K). The British Thermal Unit, or BTU, is an energy unit. The relationship is (P1/T1) = (P2/T2), where P is the pressure and T is the temperature in Kelvins. For the sake of argument, we will assume that the football is a rigid enough container (unless a ball is massively deflated, it's volume won't change). Guy-Lussac's Law describes the relationship between the pressure of a confined ideal gas and its temperature. Given the conditions of the game, a ball which meets specifications in the locker room could easily lose enough pressure to be considered under-inflated.


 0 kommentar(er)
0 kommentar(er)
