
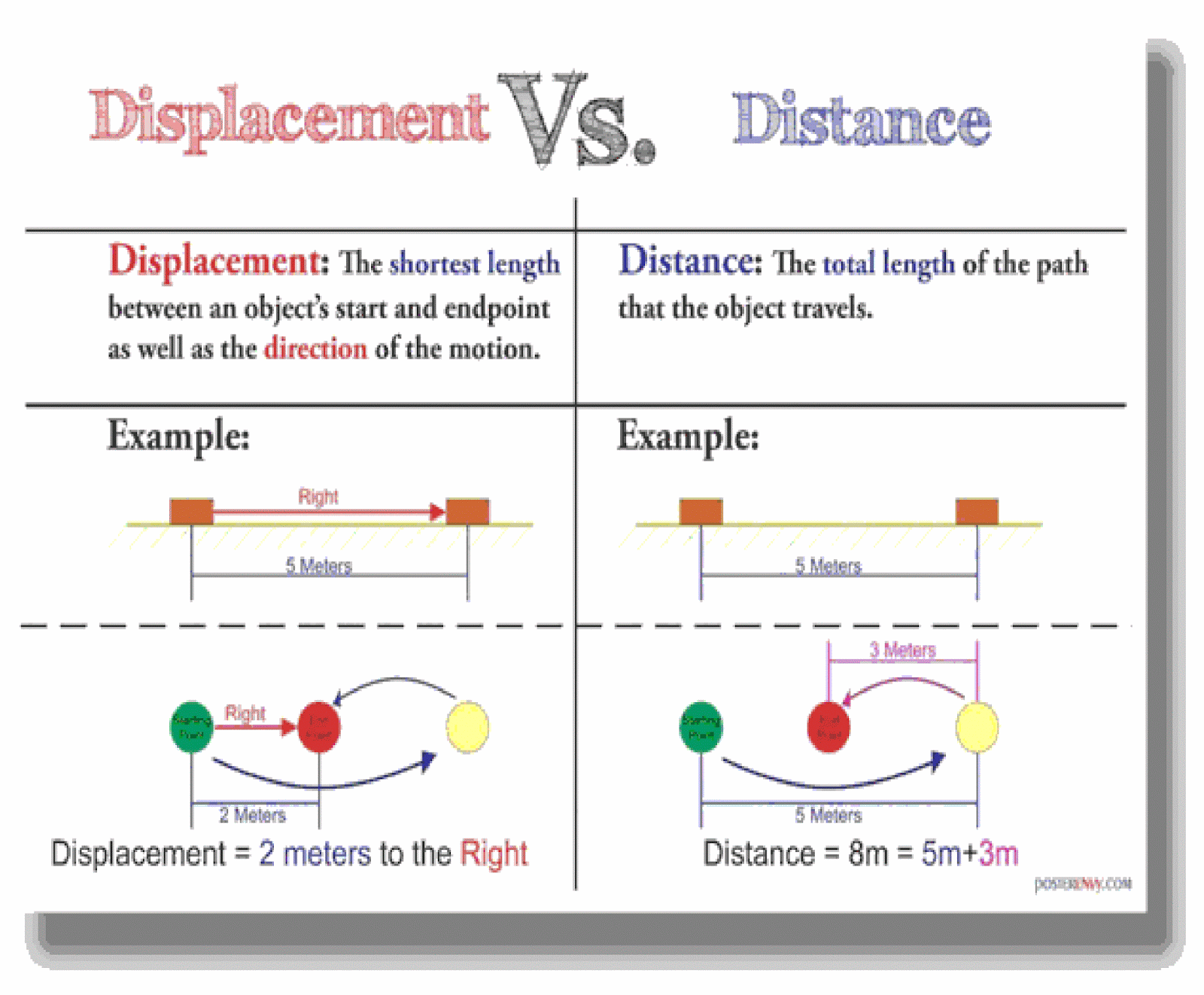
Free online physics calculators and velocity equations in terms of constant. As we stated in the Physics Tutorial 'Position.Reference Point', the position of an object is a vector, which starts at the origin and ends at the objects location.When there is any change in position, we must consider two vectors: the initial and final position vectors which both start from the origin as shown in the figure below. Solve for s, u, a or t displacement, initial velocity, acceleration or time. The fourth order derivative is called jounce. Definition: Displacement of an object from a point of reference, O is the shortest distance of the object from point O in a specific direction. Displacement in the 2-D coordinative system. Such higher-order terms are required in order to accurately represent the displacement function as a sum of an infinite series, enabling several analytical techniques in engineering and physics. So, before discussing displacement, it is important to understand how a position is denoted using vectors. To calculate displacement, you need to subtract the position vector of the initial position from the position vector of the final position. Study of these higher order derivatives can improve approximations of the original displacement function. Displacement is a vector quantity, which has both a magnitude (size) and a direction. The position vector directs from the reference. In physics terms, you often see displacement referred to as the variable s. By extension, the higher order derivatives can be computed in a similar fashion. In physics, displacement is the vector that specifies the change in position of a point, particle, or object. In physics, you find displacement by calculating the distance between an object’s initial position and its final position. Displacement is a vector quantity as it depends upon both magnitude and direction. Distance is a scalar quantity as it only depends upon the magnitude and not the direction. The SI unit for displacement is the meter (m). In this text, the Greek letter (delta) always means change in whatever quantity follows it. In symbols, displacement x is defined to be x xf xo, where xo is the initial position and xf is the final position. These common names correspond to terminology used in basic kinematics. Displacement is the direct length between any two points when measured along the minimum path between them. Displacement is the change in position of an object.


 0 kommentar(er)
0 kommentar(er)
